편직사의 놀라운 특성은 결코 놀라움을 선사하지 않으며 물론 즐거움을 선사합니다. 많은 아름다운 장난감, 베개, 심지어 물건까지 이미 만들어졌습니다. 그러나 무엇보다도 주부는 집에 필요하고 귀여운 것에 만족할 것입니다. 이것은 깔개입니다.
러그에는 얼마나 많은 뜨개질 원사가 사용됩니까?
놀라운 원사로 만든 러그에 얼마나 많은 원사가 필요한지에 관한 매우 중요한 질문입니다. 뜨개질 전문가조차도 소비에 대한 정보를 얻기 위해 반복적으로 인터넷을 사용했습니다.
실의 양을 계산하는 공식이 있나요? 실제로 원사를 계산하는 특수 계산기가 있습니다.
둥근 깔개를 단계별로 만드는 마스터 클래스에서는 직경 1미터에 다음이 필요합니다.
리본 실 5타래, 한 타래의 길이는 100미터, 한 타래의 무게는 350g입니다.
그러나 직경 1미터당 동일한 양의 실이 필요하다고 생각할 필요는 없습니다. 각 링이 증가할수록 소비도 증가합니다.
직사각형 제품의 소비량을 계산하는 것이 더 쉽습니다.
중요한! 바로 아래에는 기하학적 모양을 사용한 공식(고유한 공식)을 사용하여 원의 실 소비량을 계산하는 방법에 대한 팁이 나와 있습니다.
따라서 정사각형이나 직사각형의 변이 알려져 있습니다. 필요한 실의 양을 정확히 확인하려면 샘플을 만들어야 합니다.
샘플을 만드는 방법:
- 작은 사각형을 뜨다;
- 10cm 행에 몇 개의 요소가 있는지 측정합니다.
- 10cm에 몇 줄이 있는지 측정합니다.
두 개의 숫자를 얻으면 이것이 패턴의 편직 밀도입니다. 나중에 특별한 수학 공식에 유용하게 사용될 것입니다. 여기서 x는 작업할 알 수 없는 루프 세트와 동일한 알 수 없는 변수입니다.
비율이 작성되고 변수를 알 수 없는 방정식이 해결됩니다.
x=(a*b)/c
- a - 10cm의 루프 수;
- h - 10cm;
- s-cm 세트.
이 사각형의 경우 실의 길이를 측정하고 양탄자에 그러한 사각형이 몇 개 있는지 측면에서 계산해야합니다.
가장 큰 비밀은 이 공식과 기하학을 사용하여 실의 양을 계산하는 방법입니다. 둥근 깔개 용.
이렇게 하려면 원의 지름을 변의 길이로 결정합니다. 큰 정사각형에 필요한 밀도와 실 수를 계산하십시오. 결과적으로 원은 사각형 안에 있게 됩니다. 그리면 원의 채워진 면적이 전체 큰 사각형의 정확히 1/2과 같다는 것이 즉시 분명해집니다. 따라서 실의 수를 2로 나누기만 하면 됩니다. 이것이 바로 비밀입니다.
타원형의 작은 비밀. 이를 위해서는 타원형 부분의 측면(즉, 가장 긴 길이와 가장 작은 너비)이 있는 직사각형의 실 수를 계산해야 합니다. 그런 다음 원사 수를 2로 나눕니다.
중요한! 실을 연속적으로 가져가서는 안 되며, 섬유가 부족할 경우 적절한 색상을 찾기 위해 도시를 여기저기 운전할 필요가 없도록 항상 예비 섬유 공급량을 확보해야 합니다.
뜨개질의 비밀
뜨개질에는 많은 비밀이 있으며 경험이 풍부한 뜨개질꾼은 각자 자신의 개인적인 조언을 축적합니다. 하지만 가장 좋은 조언은 올바른 결정을 내리기 전에 직접 시도해 보는 것입니다. 어쩌면 루프 감소를 더 정확하고 눈에 띄지 않게 만들 수도 있습니다. 둥근 깔개를 뜨개질할 때 주인이 어떻게 했는지. 원형 패턴을 이용하여 둥근 러그를 만드는 패턴이 있습니다.
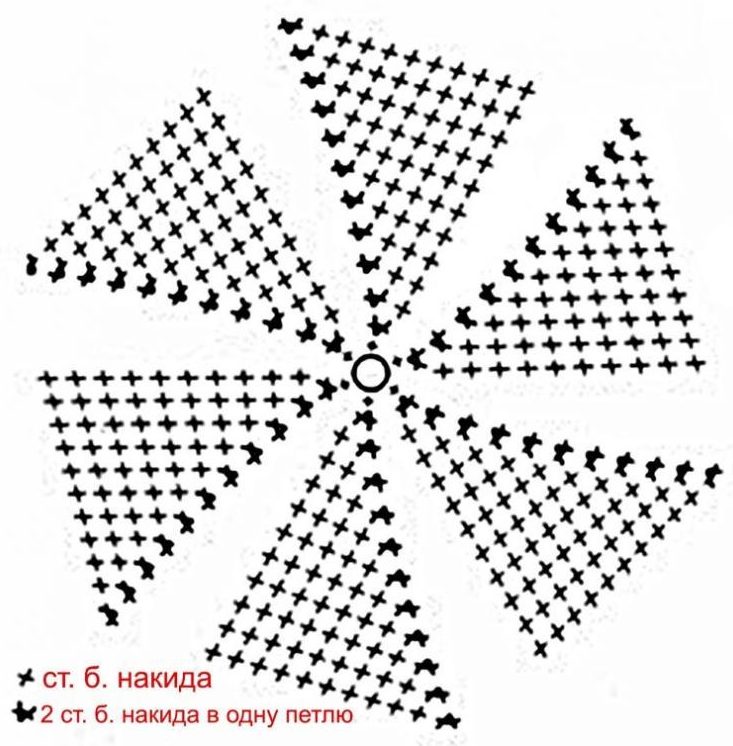실제로 이 패턴을 수행할 때 솔기가 형성되는지는 즉시 명확하지 않습니다. 항상 필요한 것은 아니며 어떤 경우에는 장인이 추가 사항을 눈에 띄지 않게 만들기 위해 노력합니다. 그러한 경우에 대한 비밀은 다음과 같습니다. 각 행에 동일한 수량으로 교대 및 추가가 필요하지만 다른 위치에서 수행해야 하며 이 경우 제품을 수행할 때 간격을 관찰하는 것이 중요합니다.
아름다운 러그를 만들고, 새로운 걸작에 딱 맞는 털실을 구입할 수 있는 확실한 방법을 찾을 수 있습니다. 많은 문헌을 읽어야 하지만 직장에서 추측하지 않도록 한 번만 시도해 볼 수 있습니다. 우리는 광범위한 경험을 가진 모든 초보 장인과 재능 있는 뜨개질꾼의 성공적인 작업을 기원합니다.
0
